| ARM Assembly Language Programming | |
| Alligata Media |
Like most interesting subjects, assembly language programming requires a little background knowledge before you can start to appreciate it. In this chapter, we explore these basics. If terms such as two's complement, hexadecimal, index register and byte are familiar to you, the chances are you can skip to the next chapter, or skim through this one for revision. Otherwise, most of the important concepts you will need to understand to start programming in assembler are explained below.
One prerequisite, even for the assembly language beginner, is a familiarity with some high-level language such as BASIC or Pascal. In explaining some of the important concepts, we make comparisons to similar ideas in BASIC, C or Pascal. If you don't have this fundamental requirement, you may as well stop reading now and have a bash at BASIC first.
1.1 Machine code and up...
The first question we need to answer is, of course, 'What is assembly language'. As you know, any programming language is a medium through which humans may give instructions to a computer. Languages such as BASIC, Pascal and C, which we call high-level languages, bear some relationship to English, and this enables humans to represent ideas in a fairly natural way. For example, the idea of performing an operation a number of times is expressed using the BASIC FOR construct:
FOR i=1 TO 10 : PRINT i : NEXT i
Although these high-level constructs enable us humans to write programs in a relatively painless way, they in fact bear little relationship to the way in which the computer performs the operations. All a computer can do is manipulate patterns of 'on' and 'off', which are usually represented by the presence or absence of an electrical signal.
To explain this seemingly unbridgable gap between electrical signals and our familiar FOR...NEXT loops, we use several levels of representation. At the lowest level we have our electrical signals. In a digital computer of the type we're interested in, a circuit may be at one of two levels, say 0 volts ('off') or 5 volts ('on').
Now we can't tell very easily just by looking what voltage a circuit is at, so we choose to write patterns of on/off voltages using some visual representation. The digits 0 and 1 are used. These digits are used because, in addition to neatly representing the idea of an absence or presence of a signal, 0 and 1 are the digits of the binary number system, which is central to the understanding of how a computer works. The term binary digit is usually abbreviated to bit. Here is a bit: 1. Here are eight bits in a row:
Machine code
Suppose we have some way of storing groups of binary digits and feeding them into the computer. On reading a particular pattern of bits, the computer will react in some way. This is absolutely deterministic; that is, every time the computer sees that pattern its response will be the same. Let's say we have a mythical computer which reads in groups of bits eight at a time, and according to the pattern of 1s and 0s in the group, performs some task. On reading this pattern, for example
10100111
the computer might produce a voltage on a wire, and on reading the pattern
10100110
it might switch off that voltage. The two patterns may then be regarded as instructions to the computer, the first meaning 'voltage on', the second 'voltage off'. Every time the instruction 10100111 is read, the voltage will come on, and whenever the pattern 10100110 is encountered, the computer turns the voltage off. Such patterns of bits are called the machine code of a computer; they are the codes which the raw machinery reacts to.
Assembly language and assemblers
There are 256 combinations of eight 1s and 0s, from 00000000 to 11111111, with 254 others in between. Remembering what each of these means is asking too much of a human: we are only good at remembering groups of at most six or seven items. To make the task of remembering the instructions a little easier, we resort to the next step in the progression towards the high-level instructions found in BASIC. Each machine code instruction is given a name, or mnemonic. Mnemonics often consist of three letters, but this is by no means obligatory. We could make up mnemonics for our two machine codes:
ON means 10100111
OFF means 10100110
So whenever we write ON in a program, we really mean 10100111, but ON is easier to remember. A program written using these textual names for instructions is called an assembly language program, and the set of mnemonics that is used to represent a computer's machine code is called the assembly language of that computer. Assembly language is the lowest level used by humans to program a computer; only an incurable masochist would program using pure machine code.
It is usual for machine codes to come in groups which perform similar functions. For example, whereas 10100111 might mean switch on the voltage at the signal called 'output 0', the very similar pattern 10101111 could mean switch on the signal called 'output 1'. Both instructions are 'ON' ones, but they affect different signals. Now we could define two mnemonics, say ON0 and ON1, but it is much more usual in assembly language to use the simple mnemonic ON and follow this with extra information saying which signal we want to switch on. For example, the assembly language instruction
ON 1
would be translated into 10101111, whereas:
ON 0
is 10100111 in machine code. The items of information which come after the mnemonic (there might be more than one) are called the operands of the instruction.
How does an assembly program, which is made up of textual information, get converted into the machine code for the computer? We write a program to do it, of course! Well, we don't write it. Whoever supplies the computer writes it for us. The program is called an assembler. The process of using an assembler to convert from mnemonics to machine code is called assembling. We shall have more to say about one particular assembler - which converts from ARM assembly language into ARM machine code - in Chapter Four.
Compilers and interpreters
As the subject of this book is ARM assembly language programming, we could halt the discussion of the various levels of instructing the computer here. However, for completeness we will briefly discuss the missing link between assembly language and, say, Pascal. The Pascal assignment
a := a+12
looks like a simple operation to us, and so it should. However, the computer knows nothing of variables called a or decimal numbers such as 12. Before the computer can do what we've asked, the assignment must be translated into a suitable sequence of instructions. Such a sequence (for some mythical computer) might be:
LOAD a
ADD 12
STORE a
Here we see three mnemonics, LOAD, ADD and STORE. LOAD obtains the value from the place we've called a, ADD adds 12 to this loaded value, and STORE saves it away again. Of course, this assembly language sequence must be converted into machine code before it can be obeyed. The three mnemonics above might convert into these instructions:
00010011
00111100
00100011
Once this machine code has been programmed into the computer, it may be obeyed, and the initial assignment carried out.
To get from Pascal to the machine code, we use another program. This is called a compiler. It is similar to an assembler in that it converts from a human-readable program into something a computer can understand. There is one important difference though: whereas there is a one-to-one relationship between an assembly language instruction and the machine code it represents, there is no such relationship between a high-level language instruction such as
PRINT "HELLO"
and the machine code a compiler produces which has the same effect. Therein lies one of the advantages of programming in assembler: you know at all times exactly what the computer is up to and have very intimate control over it. Additionally, because a compiler is only a program, the machine code it produces can rarely be as 'good' as that which a human could write.
A compiler has to produce working machine code for the infinite number of programs that can be written in the language it compiles. It is impossible to ensure that all possible high-level instructions are translated in the optimum way; faster and smaller human-written assembly language programs will always be possible. Against these advantages of using assembler must be weighed the fact that high-level languages are, by definition, easier for humans to write, read and debug (remove the errors).
The process of writing a program in a high-level language, running the compiler on it, correcting the mistakes, re-compiling it and so on is often time consuming, especially for large programs which may take several minutes (or even hours) to compile. An alternative approach is provided by another technique used to make the transition from high-level language to machine code. This technique is know as interpreting. The most popular interpreted language is BASIC.
An interpreted program is not converted from, say, BASIC text into machine code. Instead, a program (the interpreter) examines the BASIC program and decides which operations to perform to produce the desired effect. For example, to interpret the assignment
LET a=a+12
in BASIC, the interpreter would do something like the following:
| 1 | Look at the command | LET |
| 2 | This means assignment, so look for the variable to be assigned |
| 3 | Check there's an equals sign after the a |
| 4 | If not, give a Missing = error |
| 5 | Find out where the value for a is stored |
| 6 | Evaluate the expression after the = |
| 7 | Store that value in the right place for a |
Notice at step 6 we simplify things by not mentioning exactly how the expression after the = is evaluated. In reality, this step, called 'expression evaluation' can be quite a complex operation.
The advantage of operating directly on the BASIC text like this is that an interpreted language can be made interactive. This means that program lines can be changed and the effect seen immediately, without time-consuming recompilation; and the values of variables may be inspected and changed 'on the fly'. The drawback is that the interpreted program will run slower than an equivalent compiled one because of all the checking (for equals signs etc.) that has to occur every time a statement is executed. Interpreters are usually written in assembler for speed, but it is also possible to write one in a high-level language.
Summary
We can summarise what we have learnt in this section as follows. Computers understand (respond to) the presence or absence of voltages. We can represent these voltages on paper by sequences of 1s and 0s (bits). The set of bit sequences which cause the computer to respond in some well-defined way is called its machine code. Humans can't tell 10110111 from 10010111 very well, so we give short names, or mnemonics, to instructions. The set of mnemonics is the assembly language of the computer, and an assembler is a program to convert from this representation to the computer-readable machine code. A compiler does a similar job for high-level languages.
1.2 Computer architecture
So far we have avoided the question of how instructions are stored, how the computer communicates with the outside world, and what operations a typical computer is actually capable of performing. We will now clear up these points and introduce some more terminology.
The CPU
In the previous section, we used the word 'computer' to describe what is really only one component of a typical computer system. The part which reads instructions and carries them out (executes them) is called the processor, or more fully, the central processing unit (CPU). The CPU is the heart of any computer system, and in this book we are concerned with one particular type of CPU - the Acorn RISC Machine or ARM.
In most microcomputer systems, the CPU occupies a single chip (integrated circuit), housed in a plastic or ceramic package. The ARM CPU is in a square package with 84 connectors around the sides. Section 1.4 describes in some detail the major elements of the ARM CPU. In this section we are more concerned with how it connects with the rest of the system.
Computer busses
The diagram below shows how the CPU slots into the whole system:
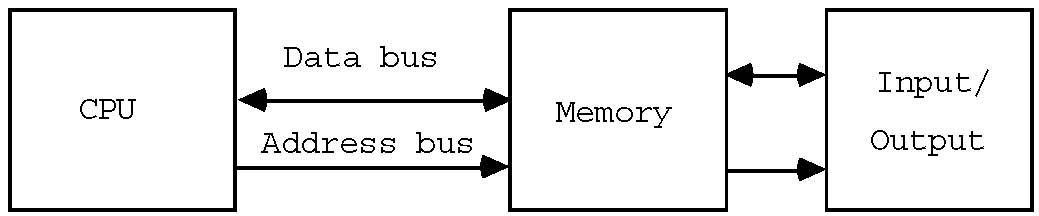
This is a much simplified diagram of a computer system, but is shows the three main components and how they are connected. The CPU has already been mentioned. Emanating from it are two busses. A bus in this context is a group of wires carrying signals. There are two of them on the diagram. The data bus is used to transfer information (data) in and out of the CPU. The address bus is produced by the CPU to tell the other devices (memory and input/output) which particular item of information is required.
Busses are said to have certain widths. This is just the number of signals that make up the bus. For a given processor the width of the data bus is usually fixed; typical values are 8, 16 and 32 bits. On the ARM the data bus is 32 bits wide (i.e. there are 32 separate signals for transferring data), and the ARM is called a 32-bit machine. The wider the data bus, the larger the amount of information that can be processed in one go by the CPU. Thus it is generally said that 32-bit computers are more powerful than 16-bit ones, which in turn are more powerful than 8-bit ones.
The ARM's address bus has 26 signals. The wider the address bus, the more memory the computer is capable of using. For each extra signal, the amount of memory possible is doubled. Many CPUs (particularly the eight-bit ones, found in many older home and desk-top micros) have a sixteen-bit address bus, allowing 65,536 memory cells to be addressed. The ARM's address bus has 26 signals, allowing over 1000 times as much memory.
As we said above, the ARM has 84 signals. 58 of these are used by the data and address busses; the remainder form yet another bus, not shown on the diagram. This is called the control signal bus, and groups together the signals required to perform tasks such as synchronising the flow of information between the ARM and the other devices.
Memory and I/O
The arrows at either end of the data bus imply that information may flow in and out of the computer. The two blocks from where information is received, and to where it is sent, are labelled Memory and Input/output. Memory is where programs, and all the information associated with them, are held. Earlier we talked about instructions being read by the CPU. Now we can see that they are read from the computer's memory, and pass along the data bus to the CPU. Similarly, when the CPU needs to read information to be processed, or to write results back, the data travels to and fro along the data bus.
Input/output (I/O) covers a multitude of devices. To be useful, a computer must communicate with the outside world. This could be via a screen and keyboard in a personal computer, or using temperature sensors and pumps if the computer happened to be controlling a central heating system. Whatever the details of the computer's I/O, the CPU interacts with it through the data bus. In fact, to many CPUs (the ARM being one) I/O devices 'look' like normal memory; this is called memory-mapped I/O.
The other bus on the diagram is the Address Bus. A computer's memory (and I/O) may be regarded as a collection of cells, each of which may contain n bits of information, where n is the width of the data bus. Some way must be provided to select any one of these cells individually. The function of the address bus is to provide a code which uniquely identifies the desired cell. We mentioned above that there are 256 combinations of eight bits, so an 8-bit address bus would enable us to uniquely identify 256 memory cells. In practice this is far too few, and real CPUs provide at least 16 bits of address bus: 65536 cells may be addressed using such a bus. As already mentioned the ARM has a 26-bit address bus, which allows 64 million cells (or 'locations') to be addressed.
Instructions
It should now be clearer how a CPU goes about its work. When the processor is started up (reset) it fetches an instruction from some fixed location. On the ARM this is the location accessed when all 26 bits of the address bus are 0. The instruction code - 32 bits of it on the ARM - is transferred from memory into the CPU. The circuitry in the CPU figures out what the instruction means (this is called decoding the instruction) and performs the appropriate action. Then, another instruction is fetched from the next location, decoded and executed, and so on. This sequence is the basis of all work done by the CPU. It is the fact that the fetch-decode-execute cycle may be performed so quickly that makes computers fast. The ARM, for example, can manage a peak of 8,000,000 cycles a second. Section
1.4 says more about the fetch-decode-execute cycle.
What kind of instructions does the ARM understand? On the whole they are rather simple, which is one reason why they can be performed so quickly. One group of instructions is concerned with simple arithmetic: adding two numbers and so on. Another group is used to load and store data into and out of the CPU. One particular instruction causes the ARM to abandon its usual sequential mode of fetching instructions and start from somewhere else in the memory. A large proportion of this book deals with detailed descriptions of all of the ARM instructions - in terms of their assembly language mnemonics rather than the 32-bit codes which are actually represented by the electric signals in the chips.
Summary
The ARM, in common with most other CPUs, is connected to memory and I/ O devices through the data bus and address bus. Memory is used to store instructions and data. I/O is used to interface the CPU to the outside world. Instructions are fetched in a normally sequential fashion, and executed by the CPU. The ARM has a 32-bit data bus, which means it usually deals with data of this size. There are 26 address signals, enabling the ARM to address 64 million memory or I/O locations.
1.3 Bits, bytes and binary
Earlier we stated the choice of the digits 0 and 1 to represent signals was important as it tied in with the binary arithmetic system. In this section we explain what binary representation is, and how the signals appearing on the data and address busses may be interpreted as binary numbers.
All data and instructions in computers are stored as sequences of ones and zeros, as mentioned above. Each binary digit, or bit, may have one of two values, just as a decimal digit may have one of the ten values 0-9.
We group bits into lots of eight. Such a group is called a byte, and each bit in the byte represents a particular value. To understand this, consider what the decimal number 3456 means:
102
103 101 100
Thousands Hundreds Tens Units
3 4 56
3000 + 400 + 50 + 6 = 3456
Each digit position represents a power of ten. The rightmost one gives the number of units (ten to the zeroth power), then the tens (ten to the one) and so on. Each column's significance is ten times greater than the one on its right. We can write numbers as big as we like by using enough digits.
Now look at the binary number 1101:
![]() 3 22 21 20
3 22 21 20
Eights Fours Twos Units
110 1
8 + 4 +0 + 1 = 13
Once again the rightmost digit represents units. The next digit represents twos (two to the one) and so on. Each column's significance is twice as great as the one on its right, and we can represent any number by using enough bits.
The way in which a sequence of bits is interpreted depends on the context in which it is used. For example, in section 1.1 we had a mythical computer which used eight-bit instructions. Upon fetching the byte 10100111 this computer caused a signal to come on. In another context, the binary number 10100111 might be one of two values which the computer is adding together. Here it is used to represent a quantity:
1*2 7 + 0*26 + 1*25 + 0*24 + 0*23 + 1*22 + 1*21 + 1*20 =
128 + 32 + 4 + 2 + 1 = 167
If we want to specify a particular bit in a number, we refer to it by the power of two which it represents. For example, the rightmost bit represents two to the zero, and so is called bit zero. This is also called the least significant bit (LSB), as it represents the smallest magnitude. Next to the LSB is bit 1, then bit 2, and so on. The highest bit of a N-bit number will be bit N-1, and naturally enough, this is called the most significant bit - MSB.
As mentioned above, bits are usually grouped into eight-bit bytes. A byte can therefore represent numbers in the range 00000000 to 11111111 in binary, or 0 to 128+64+32+16+8+4+2+1 = 255 in decimal. (We shall see how negative numbers are represented below.)
Where larger numbers are required, several bytes may be used to increase the range. For example, two bytes can represent 65536 different values and four-byte (32-bit) numbers have over 4,000,000,000 values.
As the ARM operates on 32-bit numbers, it can quite easily deal with numbers of the magnitude just mentioned. However, as we will see below, byte-sized quantities are also very useful, so the ARM can deal with single bytes too.
In addition to small integers, bytes are used to represent characters. Characters that you type at the keyboard or see on the screen are given codes. For example, the upper-case letter A is given the code 65. Thus a byte which has value 65 could be said to represent the letter A. Given that codes in the range 0-255 are available, we can represent one of 256 different characters in a byte.
In the environment under which you will probably be using the ARM, 223 of the possible codes are used to represent characters you can see on the screen. 95 of these are the usual symbols you see on the keyboard, e.g. the letters, digits and punctuation characters. Another 128 are special characters, e.g. accented letters and maths symbols. The remaining 33 are not used to represent printed characters, but have special meanings.
Binary arithmetic
Just as we can perform various operations such as addition and subtraction on decimal numbers, we can do arithmetic on binary numbers. In fact, designing circuits to perform, for example, binary addition is much easier than designing those to operate on 'decimal' signals (where we would have ten voltage levels instead of two), and this is one of the main reasons for using binary.
The rules for adding two decimal digits are:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0 carry 1
To add the two four-bit numbers 0101 and 1001 (i.e. 5+9) we would start from the right and add corresponding digits. If a carry is generated (i.e. when adding 1 and 1), it is added to the next digit on the right. For example:
0 1 0 1
+ 1 0 0 1
_______1_
1 1 1 0
= 8 + 4 + 2 = 14
Binary subtraction is defined in a similar way:
0 - 0 = 0
0 - 1 = 1 borrow 1
1 - 0 = 1
1 - 1 = 0
An example is 1001 - 0101 (9-5 in decimal):
1 0 0 1
-0 1 0 1
_1____
0 1 0 0
= 4
So far we have only talked about positive numbers. We obviously need to be able to represent negative quantities too. One way is to use one bit (usually the MSB) to represent the sign - 0 for positive and 1 for negative. This is analogous to using a + or - sign when writing decimal numbers. Unfortunately it has some drawbacks when used with binary arithmetic, so isn't very common.
The most common way of representing a negative number is to use 'two's complement' notation. We obtain the representation for a number -n simply by performing the subtraction 0 - n. For example, to obtain the two's complement notation for -4 in a four-bit number system, we would do:
0 0 0 0
-0 1 0 0
_1____
1 1 0 0
So -4 in a four-bit two's complement notation is 1100. But wait a moment! Surely 1100 is twelve? Well, yes and no. If we are using the four bits to represent an unsigned (i.e. positive) number, then yes, 1100 is twelve in decimal. If we are using two's complement notation, then half of the possible combinations (those with MSB = 1) must be used to represent the negative half of the number range. The table below compares the sixteen possible four bit numbers in unsigned and two's complement interpretation: One of the advantages of two's complement is that arithmetic works just as well for negative numbers as it does for positive ones. For example, to add 6 and -3, we would use:
| Binary | Unsigned | Two's complement |
| 0000 | 0 | 0 |
| 0001 | 1 | 1 |
| 0010 | 2 | 2 |
| 0011 | 3 | 3 |
| 0100 | 4 | 4 |
| 0101 | 5 | 5 |
| 0110 | 6 | 6 |
| 0111 | 7 | 7 |
| 1000 | 8 | -8 |
| 1001 | 9 | -7 |
| 1010 | 10 | -6 |
| 1011 | 11 | -5 |
| 1100 | 12 | -4 |
| 1101 | 13 | -3 |
| 1110 | 14 | -2 |
| 1111 | 15 | -1 |
0 1 1 0
+ 1 1 0 1
_1____
0 0 1 1 = 3
Notice that when the two MSBs were added, a carry resulted, which was ignored in the final answer. When we perform arithmetic on the computer, we can tell whether this happens and take the appropriate action.
Some final notes about two's complement. The width of the number is important. For example, although 1100 represents -4 in a four-bit system, 01100 is +14 is a five-bit system. -4 would be 11100 as a five bit number. On the ARM, as operations are on 32-bit numbers, the two's complement range is approximately -2,000,000,000 to +2,000,000,000.
The number -1 is always 'all ones', i.e. 1111 in a four-bit system, 11111111 in eight bits etc.
To find the negative version of a number n, invert all of its bits (i.e. make all the 1s into 0s and vice versa) and add 1. For example, to find -10 in an eight-bit two's complement form:
10 is 00001010
inverted is 11110101
plus 1 is 11110110
Hexadecimal
It is boring to have to write numbers in binary as they get so long and hard to remember. Decimal could be used, but this tends to hide the significance of individual bits in a number. For example, 110110 and 100110 look as though they are connected in binary, having only one different bit, but their decimal equivalents 54 and 38 don't look at all related.
To get around this problem, we often call on the services of yet another number base, 16 or hexadecimal. The theory is just the same as with binary and decimal, with each hexadecimal digit having one of sixteen different values. We run out of normal digits at 9, so the letters A-F are used to represent the values between 11 and 15 (in decimal). The table below shows the first sixteen numbers in all three bases: Hexadecimal (or hex, as it is usually abbreviated) numbers are preceded by an ampersand & in this book to distinguish them from decimal numbers. For example, the hex number &D9F is 13*162 + 9*16 + 15 or 3487.
| Decimal | Binary | Hexadecimal |
| 0 | 0000 | 00 |
| 1 | 0001 | 01 |
| 2 | 0010 | 02 |
| 3 | 0011 | 03 |
| 4 | 0100 | 04 |
| 5 | 0101 | 05 |
| 6 | 0110 | 06 |
| 7 | 0111 | 07 |
| 8 | 1000 | 08 |
| 9 | 1001 | 09 |
| 10 | 1010 | 0A |
| 11 | 1011 | 0B |
| 12 | 1100 | 0C |
| 13 | 1101 | 0D |
| 14 | 1110 | 0E |
| 15 | 1111 | 0F |
The good thing about hex is that it is very easy to convert between hex and binary representation. Each hexadecimal digit is formed from four binary digits grouped from the left. For example:
11010110 = 1101 0110 = D 6 = &D6
11110110 = 1001 0110 = F 6 = &F6
The examples show that a small change in the binary version of a number produces a small change in the hexadecimal representation.
The ranges of numbers that can be held in various byte multiples are also easy to represent in hex. A single byte holds a number in the range &00 to &FF, two bytes in the range &0000 to &FFFF and four bytes in the range &00000000 to &FFFFFFFF.
As with binary, whether a given hex number represents a negative quantity is a matter of interpretation. For example, the byte &FE may represent 254 or -2, depending on how we wish to interpret it.
Large numbers
We often refer to large quantities. To save having to type, for example 65536, too frequently, we use a couple of useful abbreviations. The letter K after a number means 'Kilo' or 'times 1024'. (Note this Kilo is slightly larger than the kilo (1000) used in kilogramme etc.) 1024 is two to the power ten and is a convenient unit when discussing, say, memory capacities. For example, one might say 'The BBC Micro Model B has 32K bytes of RAM,' meaning 32*1024 or 32768 bytes.
For even larger numbers, mega (abbr. M) is used to represent 1024*1024 or just over one million. An example is 'This computer has 1M byte of RAM.'
Memory and addresses
The memory of the ARM is organised as bytes. Each byte has its own address, starting from 0. The theoretical upper limit on the number of bytes the ARM can access is determined by the width of the address bus. This is 26 bits, so the highest address is (deep breath) 11111111111111111111111111 or &3FFFFFF or 67,108,863. This enables the ARM to access 64M bytes of memory. In practice, a typical system will have one or four megabytes, still a very reasonable amount.
The ARM is referred to as a 32-bit micro. This means that it deals with data in 32-bit or four-byte units. Each such unit is called a word (and 32-bits is the word-length of the ARM). Memory is organised as words, but can be accessed either as words or bytes. The ARM is a byte-addressable machine, because every single byte in memory has its own address, in the sequence 0, 1, 2 , and so on.
When complete words are accessed (e.g. when loading an instruction), the ARM requires a word-aligned address, that is, one which is a multiple of four bytes. So the first complete word is at address 0, the second at address 4, and so on.
The way in which each word is used depends entirely on the whim of the programmer. For example, a given word could be used to hold an instruction, four characters, or a single 32-bit number, or 32 one-bit numbers. It may even be used to store the address of another word. The ARM does not put any interpretation on the contents of memory, only the programmer does.
When multiple bytes are used to store large numbers, there are two ways in which the bytes may be organised. The (slightly) more common way - used by the ARM - is to store the bytes in order of increasing significance. For example, a 32-bit number stored at addresses 8..11 will have bits 0..7 at address 8, bits 8..15 at address 9, bits 16..23 at address 10, and bits 24..31 at address 11.
If two consecutive words are used to store a 64-bit number, the first word would contain bits 0..31 and the second word bits 32..63.
There are two main types of memory. The programs you will write and the data associated with them are stored in read/write memory. As its name implies, this may be written to (i.e. altered) or read from. The common abbreviation for read/write memory is RAM. This comes from the somewhat misleading term Random Access Memory. All memory used by ARMs is Random Access, whether it is read/write or not, but RAM is universally accepted to mean read/write.
RAM is generally volatile, that is, its contents are forgotten when the power is removed. Most machines provide a small amount of non-volatile memory (powered by a rechargeable battery when the mains is switched off) to store information which is only changed very rarely, e.g. preferences about the keyboard auto-repeat rate.
The other type of memory is ROM - Read-only memory. This is used to store instructions and data which must not be erased, even when the power is removed. For example the program which is obeyed when the ARM is first turned on is held in ROM.
Summary
We have seen that computers use the binary number system due to the 'twolevel' nature of the circuits from which they are constructed. Binary arithmetic is simple to implement in chips. To make life easier for humans we use hexadecimal notation to write down numbers such as addresses which would contain many bits, and assembly language to avoid having to remember the binary instruction codes.
The memory organisation of the ARM consists of 16 megawords, each of which contains four individually addressable bytes.
1.4 Inside the CPU
In this section we delve into the CPU, which has been presented only as a black box so far. We know already that the CPU presents two busses to the outside world. The data bus is used to transfer data and instructions between the CPU and memory or I/O. The address contains the address of the current location being accessed.
There are many other signals emanating from CPU. Examples of such signals on the ARM are r/w which tells the outside world whether the CPU is reading or writing data; b/w which indicates whether a data transfer is to operate on just one byte or a whole word; and two signals which indicate which of four possible 'modes' the ARM is in.
If we could examine the circuitry of the processor we would see thousands of transistors, connected to form common logic circuits. These go by names such as NAND gate, flip-flop, barrel shifter and arithmetic-logic unit (ALU).
Luckily for us programmers, the signals and components mentioned in the two previous paragraphs are of very little interest. What interests us is the way all of these combine to form an abstract model whose behaviour we can control by writing programs. This is called the 'programmers' model', and it describes the processor in terms of what appears to the programmer, rather than the circuits used to implement it.
The next chapter describes in detail the programmers' model of the ARM. In this section, we will complete our simplified look at computer architecture by outlining the purpose of the main blocks in the CPU. As mentioned above, a knowledge of these blocks isn't vital to write programs in assembly language. However, some of the terms do crop up later, so there's no harm in learning about them.
The instruction cycle
We have already mentioned the fetch-decode-execute cycle which the CPU performs continuously. Here it is in more detail, starting from when the CPU is reset.
Inside the CPU is a 24-bit store that acts as a counter. On reset, it is set to &000000. The counter holds the address of the next instruction to be fetched. It is called the program counter (PC). When the processor is ready to read the next instruction from memory, it places the contents of the PC on to the address bus. In particular, the PC is placed on bits 2..25 of the address bus. Bits 0 and 1 are always 0 when the CPU fetches an instruction, as instructions are always on word addresses, i.e. multiples of four bytes.
The CPU also outputs signals telling the memory that this is a read operation, and that it requires a whole word (as opposed to a single byte). The memory system responds to these signals by placing the contents of the addressed cell on to the data bus, where it can be read by the processor. Remember that the data bus is 32 bits wide, so an instruction can be read in one read operation.
From the data bus, the instruction is transferred into the first stage of a three-stage storage area inside the CPU. This is called the pipeline, and at any time it can hold three instructions: the one just fetched, the one being decoded, and the one being executed. After an instruction has finished executing, the pipeline is shifted up one place, so the just-decoded instruction starts to be executed, the previously fetched instruction starts to be decoded, and the next instruction is fetched from memory.
Decoding the instruction involves deciding exactly what needs to be done, and preparing parts of the CPU for this. For example, if the instruction is an addition, the two numbers to be added will be obtained.
When an instruction reaches the execute stage of the pipeline, the appropriate actions take place, a subtraction for example, and the next instruction, which has already been decoded, is executed. Also, the PC is incremented to allow the next instruction to be fetched.
In some circumstances, it is not possible to execute the next pipelined instruction because of the effect of the last one. Some instructions explicitly alter the value of the PC, causing the program to jump (like a GOTO in BASIC). When this occurs, the pre-fetched instruction is not the correct one to execute, and the pipeline has to be flushed (emptied), and the fetch-decode-cycle started from the new location. Flushing the pipeline tends to slow down execution (because the fetch, decode and execute cycles no longer all happen at the same time) so the ARM provides ways of avoiding many of the jumps.
The ALU and barrel shifter
Many ARM instructions make use of these two very important parts of the CPU. There is a whole class of instructions, called the data manipulation group, which use these units. The arithmetic-logic unit performs operations such as addition, subtraction and comparison. These are the arithmetic operations. Logical operations include AND, EOR and OR, which are described in the next chapter.
The ALU can be regarded as a black-box which takes two 32-bit numbers as input, and produces a 32-bit result. The instruction decode circuitry tells the ALU which of its repertoire of operations to perform by examining the instruction. It also works out where to find the two input numbers - the operands - and where to put the result from the instruction.
The barrel shifter has two inputs - a 32-bit word to be shifted and a count and one output - another 32-bit word. As its name implies, the barrel shifter obtains its output by shifting the bits of the operand in some way. There are several flavours of shift: which direction the bits are shifted in, whether the bits coming out of one end re-appear in the other end etc. The varieties of shift operation on the ARM are described in the next chapter.
The important property of the barrel shifter is that no matter what type of shift it does, and by how many bits, it always takes only one 'tick' of the CPU's master clock to do it. This is much better than many 16 and 32-bit processors, which take a time proportional to the number of shifts required.
Registers
When we talked about data being transferred from memory to the CPU, we didn't mention exactly where in the CPU the data went. An important part of the CPU is the register bank. In fact, from the programmer's point of view, the registers are more important than other components such as the ALU, as they are what he actually 'sees' when writing programs.
A register is a word of storage, like a memory location. On the ARM, all registers are one word long, i.e. 32 bits. There are several important differences between memory and registers. Firstly, registers are not 'memory mapped', that is they don't have 26-bit addresses like the rest of storage and I/O on the ARM.
Because registers are on the CPU chip rather than part of an external memory system, the CPU can access their contents very quickly. In fact, almost all operations on the ARM involve the use of registers. For example, the ADD instruction adds two 32-bit numbers to produce a 32-bit result. Both of the numbers to be added, and the destination of the result, are specified as ARM registers. Many CPUs also have instructions to, for example, add a number stored in memory to a register. This is not the case on the ARM, and the only register-memory operations are load and store ones.
The third difference is that there are far fewer registers than memory locations. As we stated earlier, the ARM can address up to 64M bytes (16M words) of external memory. Internally, there are only 16 registers visible at once. These are referred to in programs as R0 to 15. A couple of the registers are sometimes given special names; for example R15 is also called PC, because it holds the program counter value that we mentioned above.
As we shall see in the next chapter, you can generally use any of the registers to hold operands and results, there being no distinction for example between R0 and R12. This availability of a large (compared to many CPUs) number of rapidly accessible registers contributes to the ARM's reputation as a fast processor.
1.5 A small program
This chapter would be irredeemably tedious if we didn't include at least one example of an assembly language program. Although we haven't actually met the ARM's set of instructions yet, you should be able to make some sense of the simple program below.
On the left is a listing of a simple BASIC FOR loop which prints 20 stars on the screen. On the right is the ARM assembly language program which performs the same task.
| BASIC | ARM Assembly Language |
| 10 i=1 | MOV R0,#1 | ;Initialise count |
| 20 PRINT "*"; | .loopSWI writeI+"*" ;Print a * |
| 30 i=i+1 | ADD R0,R0,#1 | ;Increment count |
| 40 IF i<=20 THEN 20 CMP R0,#20 | ;Compare with limit |
| BLE loop | ;Repeat if required |
Even if this is the first assembly language program you have seen, most of the ARM instructions should be self-explanatory. The word loop marks the place in the program which is used by the BLE (branch if less than or equal to) instruction. It is called a label, and fulfils a similar function to the line number in a BASIC instruction such as GOTO 20.
One thing you will notice about the ARM program is that it is a line longer than the BASIC one. This is because in general, a single ARM instruction does less processing than a BASIC one. For example, the BASIC IF statement performs the function of the two ARM instructions CMP and BLE. Almost invariably, a program written in assembler will occupy more lines than an equivalent one written in BASIC or some other high-level language, usually by a much bigger ratio than the one illustrated.
However, when assembled, the ARM program above will occupy five words (one per instruction) or 20 bytes. The BASIC program, as shown, takes 50 bytes, so the size of the assembly language program (the 'source') can be misleading. Furthermore, a compiled language version of the program, for example, one in Pascal:
for i := 1 to 20 do
write('*');
occupies even fewer source lines, but when compiled into ARM machine code will use many more than 5 instructions - the exact number depending on how good the compiler is.
1.6 Summary of chapter 1
For the reader new to assembly language programming, this chapter has introduced many concepts, some of them difficult to grasp on the first reading. We have seen how computers - or the CPU in particular - reads instructions from memory and executes then. The instructions are simply patterns of 1s and 0s, which are manifestly difficult for humans to deal with efficiently. Thus we have several levels of representation, each one being further from what the CPU sees and closer to our ideal programming language, which would be an unambiguous version of English.
The lowest level of representation that humans use, and the subject of this book, is assembly language. In this language, each processor instruction is given a name, or mnemonic, which is easier to remember than a sequence of binary digits. An assembly program is a list of mnemonic instructions, plus some other items such as labels and operands. The program is converted into CPU-processable binary form by a program called an assembler. Unlike high-level languages, there is a one-to-one correspondence between assembly instructions and binary instructions.
We learned about binary representation of numbers, both signed and unsigned, and saw how simple arithmetic operations such as addition and subtraction may be performed on them.
Next, we looked inside the CPU to better understand what goes on when an instruction is fetched from memory and executed. Major components of the CPU such as the ALU and barrel shifter were mentioned. A knowledge of these is not vital for programming in assembler, but as the terms crop up in the detailed description of the ARM's instruction set, it is useful to know them.
Finally, we presented a very small assembly language program to compare and contrast it with a functionally equivalent program written in BASIC.


